صيغة القيمة المستقبلية للمعاش السنوي المستحق

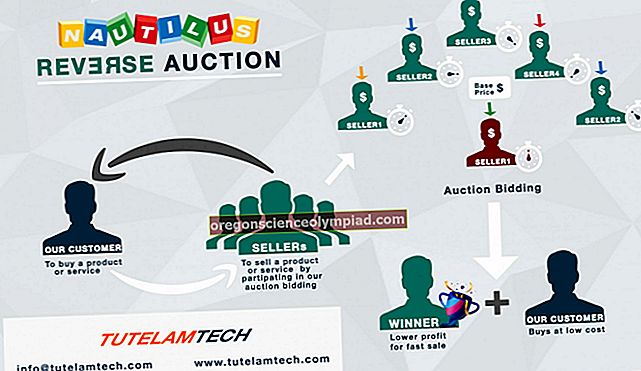
القيمة المستقبلية هي قيمة مبلغ نقدي يتم دفعه في تاريخ محدد في المستقبل. القسط السنوي المستحق عبارة عن سلسلة من المدفوعات التي يتم سدادها في بداية كل فترة في هذه السلسلة. لذلك ، تشير صيغة القيمة المستقبلية للمعاش السنوي المستحق إلى القيمة في تاريخ مستقبلي محدد لسلسلة من المدفوعات الدورية ، حيث يتم إجراء كل دفعة في بداية الفترة. هذا التدفق من المدفوعات هو سمة مشتركة للمدفوعات المقدمة للمستفيد من خطة المعاشات التقاعدية. يتم استخدام هذه الحسابات من قبل المؤسسات المالية لتحديد التدفقات النقدية المرتبطة بمنتجاتها.

صيغة حساب القيمة المستقبلية للمعاش السنوي المستحق (حيث يتم إجراء سلسلة من المدفوعات المتساوية في بداية كل فترة من الفترات المتتالية المتعددة) هي:

P = (PMT [((1 + r) n - 1) / r]) (1 + r)

أين:

P = القيمة المستقبلية لتدفق الأقساط التي يتعين دفعها في المستقبل

PMT = مبلغ كل دفعة سنوية

r = سعر الفائدة

n = عدد الفترات التي يتم خلالها سداد المدفوعات

هذه القيمة هي المبلغ الذي سينمو إليه تدفق المدفوعات المستقبلية ، بافتراض أن مبلغًا معينًا من أرباح الفوائد المركبة يتراكم تدريجياً خلال فترة القياس. الحساب مطابق للحساب المستخدم للقيمة المستقبلية للمعاش السنوي العادي ، باستثناء أننا نضيف فترة إضافية لحساب المدفوعات التي يتم إجراؤها في بداية كل فترة ، بدلاً من نهايتها.

على سبيل المثال ، يتوقع أمين خزانة ABC Imports استثمار 50000 دولار من أموال الشركة في أداة استثمار طويلة الأجل في بداية كل عام على مدى السنوات الخمس المقبلة. ويتوقع أن تكسب الشركة 6٪ فائدة تتضاعف سنويًا. يتم احتساب القيمة التي يجب أن تكون لهذه المدفوعات في نهاية فترة الخمس سنوات على النحو التالي:

P = ($ 50،000 [((1 + .06) 5-1) / .06]) (1 + .06)

P = 298.765.90 دولار

وكمثال آخر ، ماذا لو تضاعفت الفائدة على الاستثمار شهريًا وليس سنويًا ، وكان المبلغ المستثمر 4000 دولار في نهاية كل شهر؟ الحساب هو:

الاحتمال = (4000 دولار أمريكي [((1 + .005) 60-1) / .06]) (1 + .005)

P = 280475.50 دولارًا

معدل الفائدة .005 المستخدم في المثال الأخير هو 1/12 من معدل الفائدة السنوي الكامل البالغ 6٪.